
इस पृष्ठ की प्रत्येक वस्तु को एक हाउस ब्यूटीफुल एडिटर द्वारा हाथ से उठाया गया था। हम आपके द्वारा चुनी गई कुछ वस्तुओं पर कमीशन कमा सकते हैं।
काफी कुछ ऐसा नहीं है गणित की समस्या, मन झुकने ऑप्टिकल भ्रम, या गोधूलि तर्क पहेली में सभी उत्पादकता को रोकने के लिए लोकप्रिय यांत्रिकी कार्यालय। हम स्वभाव से जिज्ञासु लोग हैं, लेकिन हम सामूहिक रूप से एक जिद भी साझा करते हैं कि हम क्या हैं ठीक है, अरे, और इसलिए जब भी हम कई संभव समाधानों के साथ समस्या पर आते हैं, तो हम सड़क के किनारे काम फेंक देते हैं।
यह त्रिभुज मस्तिष्क का टीज़र नया नहीं है - PopSugar के लिये यह पता लगाना कुछ साल पहले-लेकिन कुछ छायादार इंटरनेट जादू पर आधारित, नीचे दिया गया ट्वीट आज मेरे फीड में फिर से दिखाई दिया और हमारे स्टाफ-वाइड पर एक नई बहस शुरू हुई सुस्त चैनल, एक जगह जो परंपरागत रूप से काम करने वाले विचारों के लिए आरक्षित है, लेकिन इसके बजाय ज्यादातर अन्य सामानों के बारे में चिल्लाने के लिए उपयोग की जाती है जिन्हें हम कभी-कभी बदल देते हैं सामग्री।
कहते हैं? pic.twitter.com/lrhXrWw5EP
- जे (@jiteshpillaai) 9 अप्रैल 2018
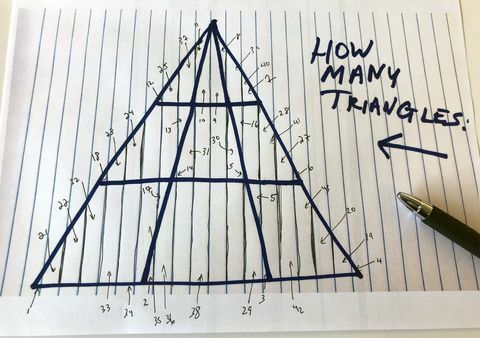
क्योंकि मैं एक मसोकिस्ट हूं, मैंने त्रिकोण को फिर से आकर्षित किया और कर्मचारियों पर सभी को तुरंत ड्रॉप करने के लिए कहा कि वे क्या कर रहे थे और सरल प्रश्न को हल करने का प्रयास करें: आप कितने त्रिकोण खोज सकते हैं?
मैं आपको पूरी बातचीत से दूर कर दूंगा - मुझ पर विश्वास करें, कोई भी उसे देखना नहीं चाहता है - लेकिन टीम की प्रतिक्रियाएं पूरे स्थान पर थीं। कुछ संपादकों ने चार त्रिकोण देखे। अन्य ने 12 देखे। कुछ ने 6, 16, 22 को देखा। और भी देखा 18। एक ज्ञानी ने प्रश्न में ही A के त्रिभुजों को गिना, जबकि दूसरे को अस्तित्वमान प्रतीत हो रहा था संकट: "इनमें से कोई भी रेखा वास्तव में सीधी नहीं है, बस घटता है - इस प्रकार आप उनमें से किसी को भी त्रिकोण के रूप में परिभाषित नहीं कर सकते हैं," उन्होंने कहा कहा हुआ। “इस तस्वीर में कोई त्रिकोण नहीं हैं। जीवन का कोई अर्थ नहीं है। ”
हमने तब अपने इंस्टाग्राम फॉलोअर्स को समस्या बताई, जिनके जवाबों ने भी सरगम को दौड़ाया, 5 से 14 तक। जबकि हम यहां ट्रोलिंग की उच्च संभावना को स्वीकार करते हैं, यह स्पष्ट है कि लोग समस्या के कई अलग-अलग तरीकों से प्रतिक्रिया देते हैं।
इस पोस्ट को इंस्टाग्राम पर देखें
कृपया रोकें कि आप क्या कर रहे हैं और हमें एक बहस को हल करने में मदद करें जो हम कार्यालय में कर रहे हैं। आप यहां कितने त्रिभुज देखते हैं?
द्वारा साझा की गई एक पोस्ट लोकप्रिय यांत्रिकी पत्रिका (@popularmechanics) पर
मैं अपने सहयोगियों को पूरे दिन उनकी संदिग्ध प्रक्रियाओं के बारे में सुनता रहा, लेकिन इसके बजाय, मैं कई ज्यामिति विशेषज्ञों के पास यह देखने के लिए पहुंचा कि क्या हम एक आम सहमति के उत्तर पर पहुंच सकते हैं। लगभग सभी गणितज्ञों से संपर्क करने पर मुझे पता चला कि उन्होंने एक ही हल खोजा- लेकिन उनमें से सभी ने एक ही तरीके से इसका पता नहीं लगाया।
यदि आप अभी तक इसका उत्तर नहीं जानना चाहते हैं, तो पढ़ना बंद कर दें और समस्या को हल करने का प्रयास करें। जब आप कर लेंगे तो मैं आपसे यहाँ वापस मिलूंगा
अरे, यह तो जल्दी थी। उत्तर के लिए तैयार हैं? कुछ के विपरीत वायरल गणित की समस्याएं जो जानबूझकर अस्पष्ट और व्याख्या के लिए खुले हैं, यह वास्तव में एक स्लैम-डंक है, इसमें कोई संदेह नहीं है, यह समाधान है, और यह है 18. आइए कुछ ज्यामिति विशेषज्ञों से क्यों इस बारे में सुनें।
"मैं इसे किसी भी गणितीय समस्या से संपर्क करने के लिए कहूंगा: इसे कम करें और संरचना खोजें," कहते हैं सिल्वेस्टर एरिकसन-बीक, पीएचडी, कैलिफोर्निया यूनिवर्सिटी लॉस एंजिल्स के गणित के साथ पोस्टडॉक्टरल फेलो विभाग।
एरिकक्सन-बिस्क कहते हैं कि जिस आकृति को मैंने आकर्षित किया, उसमें त्रिकोण बनाने का एकमात्र तरीका है, यदि शीर्ष शीर्ष (कोने) त्रिकोण का हिस्सा है। त्रिभुज का आधार तब तीन स्तरों में से एक होगा। “तीन स्तर हैं, और प्रत्येक पर आप छह अलग-अलग तरीकों के बीच एक आधार चुन सकते हैं। यह 18 या 3 गुना 6 त्रिकोण देता है। ”
आइए मास्टर त्रिकोण को फिर से देखें।
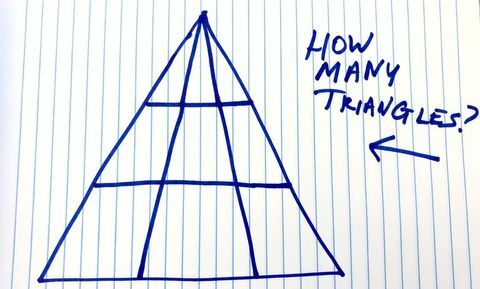
एंड्रयू डेनियल
"यह उस मामले के लिए सामान्य करने के लिए सुविधाजनक है जहाँ पर हैं n शीर्ष शीर्ष से होकर गुजरने वाली रेखाएँ, और पी क्षैतिज रेखाएं, ”फ्रांसिस बोनाहोन, पीएचडी कहते हैं, दक्षिणी कैलिफोर्निया विश्वविद्यालय में गणित के प्रोफेसर हैं।
हमारे मामले में, n = 4, और पी = 3। किसी भी त्रिभुज को हम ड्राइंग में पाते हैं एक शीर्ष शीर्ष और दो अन्य एक ही क्षैतिज रेखा पर होना चाहिए, इसलिए प्रत्येक क्षैतिज रेखा के लिए, त्रिकोण की संख्या बॉनहोन कहते हैं, '' उस लाइन पर दो कोने, इन तिराहों को चुनने के तरीकों की संख्या के बराबर हैं, बोनाहोन कहते हैं- उन तरीकों की संख्या जिनसे हम दो अलग-अलग बिंदुओं को चुन सकते हैं n, या "n 2. चुनें
हाई स्कूल का गणित याद है? यही कारण है कि के n(n-1)/2. और जब से हैं पी बोनाहन कहते हैं, यह क्षैतिज रेखा है पी एन(n-1) / 2 संभव त्रिकोण। हमारे मामले में, यह 3x4 (4-1) / 2 = 18 है।
यहां प्रत्येक संभावित त्रिकोण को खोजने का एक आसान तरीका है:
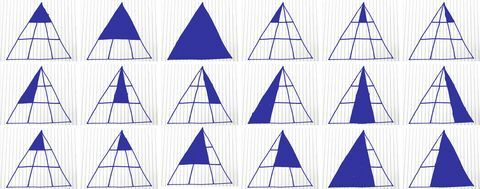
कोरी कैनेडी
जोहान मंगाहास, Ph। D., बफ़ेलो विश्वविद्यालय में एक सहायक गणित प्रोफेसर, भी 18 से पहले आए - सरल ब्रूट-बल गिनती के माध्यम से, फिर उसी चालाक के माध्यम से उपरोक्त के रूप में कॉम्बिनेटरिक्स - लेकिन हमारे त्रिकोण मस्तिष्क टीज़र को पीओ-शेन लोह, पीएच.डी., कार्नेगी मेलन विश्वविद्यालय के गणित के प्रोफेसर के रूप में काफी अच्छा नहीं मानते हैं। पिट्सबर्ग, के रूप में में चित्रित किया गया न्यूयॉर्क टाइम्सपिछले साल:
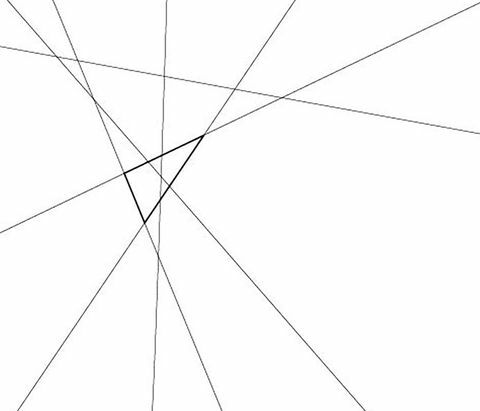
पो-शेन लोह
यह एक चालाक गणितीय उत्तर है, वह कहती है, क्योंकि यहाँ, त्रिकोण की गिनती एक ही बात है जैसे कि छह में से तीन रेखाओं के संयोजन की गणना [6-चुनें-3 = (6 * 5 * 4) / (3 * 2 * 1)]।
मंगहास कहते हैं, "उस स्थिति में, प्रत्येक जोड़ी रेखाएं प्रतिच्छेदन करती हैं और कोई ट्रिपल या अधिक चौराहे नहीं होते हैं, इसलिए तीनों में से कोई भी विकल्प हमेशा एक त्रिकोण देता है।" मैंने उसे जो चित्र भेजा था, उसमें कुछ पंक्तियाँ समानांतर हैं, इसलिए वे उसी त्रिभुज का हिस्सा नहीं हो सकते। "यदि आप एक ही सात लाइनें लेते हैं और उन्हें थोड़ा हिलाते हैं, तो संभावित रूप से वे सबसे अधिक संभावना रखते हैं [लोह की] समस्या जैसी भूमि और आपके पास अधिक त्रिकोण और एक समान प्यारा उत्तर है। "(रिकॉर्ड के लिए: 35.)
वाह। मैंने अपने सहकर्मियों के साथ इस नई त्रिकोण समस्या को अभी तक साझा नहीं किया है। लेकिन यह केवल कुछ ही समय पहले की बात है जब वे इसे खोजते हैं - और कुछ और बहस करते हैं
🚨महत्वपूर्ण अद्यतन 1/30/20This: इस कहानी को प्रकाशित करने के बाद से कई, अनेक पाठक मुझे यह बताने के लिए पहुँच गए हैं कि जबकि 18 वास्तव में इस समस्या का स्वीकार्य उत्तर है, यह नहीं है केवल एक, मेरी ओर से कुछ अनजाने निरीक्षण के कारण। मैं पाठकों पर यह बहुत आसान बना सकता था — और, मेरे इनबॉक्स पर, बहुत आसान, मैंने सिर्फ सादे, श्वेत कंप्यूटर पेपर पर त्रिभुज को तिरछा किया था। लेकिन नहीं।
मैंने दुर्भाग्य से इस त्रिकोण को पंक्तिबद्ध कागज पर आकर्षित किया, और बहुत सारे स्मार्ट लोगों ने सही ढंग से बताया है कि, ठीक है, वास्तव में, यदि आप मार्कर में लिखी गई गहरी नीली रेखाओं के अलावा छवि में हल्की नीली समानांतर रेखाओं की गिनती करते हैं, तो वास्तव में यहाँ कुल 18 से अधिक त्रिकोण हैं - बहुत अधिक। मैंने कभी भी केवल उन गहरी नीली रेखाओं का उपयोग करने के लिए निर्दिष्ट नहीं किया, और इस प्रकार, मैं गलत हूं। तुम सही हो।
एक पाठक, राल्फ लिंसंगन ने पूरी तरह से इस छवि को भेजकर मुझे स्वामित्व दिया, जिसमें उन्होंने तकनीकी के तहत पाए जाने वाले प्रत्येक अतिरिक्त त्रिकोण को चिह्नित किया, जो कुल 35 के लिए 17 अतिरिक्त त्रिकोणों को चिह्नित करता है। देखो:
इस तरह का समर्पण मुझे प्यार करने के कई कारणों में से एक है लोकप्रिय यांत्रिकी पाठकों। हम आप लोगों के सामने कुछ भी नहीं पा सकते। अगले टीज़र तक!
🚨YET ANOTHER TRIANGLE UPDATE 1/31/20 TR: अंतिम अद्यतन पोस्ट करने के बाद से, मैंने भी सुना है अधिक तुम्हारा, मुझे और आपके साथी पाठकों को लगातार धोखा देते रहना चाहिए - अतिरिक्त संभावित त्रिकोणों पर विचार नहीं करने के लिए। पाठक डेरेक श्नाइडर की बात सुनें, जिन्होंने एक अन्य ग्राफिक में सुझाव दिया था कि 45 त्रिकोण हैं।
अगर हम मूल नियमों का पालन करते हैं, तो मैं गिनती करता हूं और अतिरिक्त 9 जो निश्चित हैं (हरे रंग में) और एक ऐसा आप कैसे शीर्ष स्थान (बैंगनी में) को नेत्रहीन स्थान के आधार पर व्याख्या के लिए खुले रहें... मैं व्यक्तिगत रूप से गिनूंगा यह।
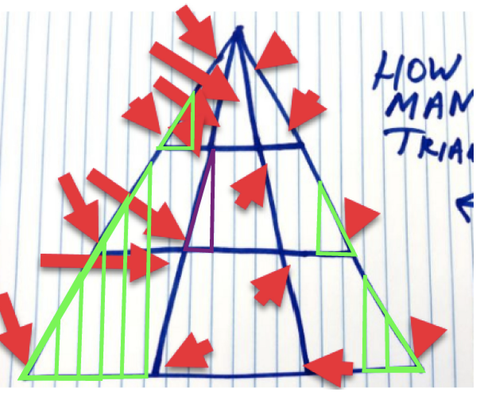
डेरेक श्नाइडर
इस बीच, पाठक ने कहा, यह कहने के लिए कि हम सभी के साथ त्रिकोण की गिनती में "गंभीर त्रुटि" कर रहे हैं:
उदाहरण के लिए, नीचे दायां कोना लें, यह एक त्रिकोण के लिए एक तीर दिखाता है। हालाँकि, ये हल्की नीली रेखाएं इस अकेले एक कोने में लगभग तीन त्रिभुज बना सकती हैं:

Poingly
हालांकि इनमें से कुछ MAY कुछ डिबेटेबल हो सकते हैं (यानी, जहां हल्की नीली लाइनें अंधेरे को काटती हैं और करती हैं वे तकनीकी रूप से एक त्रिभुज या एक चतुर्भुज बनाते हैं), मैंने SEVEN ADDITIONAL त्रिकोण की गणना की है जो इस में बनाया जा सकता है मार्ग। यह कुल त्रिकोणों की संख्या 42 तक लाता है।
बुरी खबर यह है कि हम कुछ त्रिकोणों से चूक गए। अच्छी खबर यह है कि यह इस बात की पुष्टि करता है कि जीवन स्पष्ट रूप से सही अर्थ है, जैसा कि सटीक संख्या: 42 से स्पष्ट है।
बकाया बिंदु, सहसा। पाठक जेम्स गुडरिच ने एक और कदम आगे बढ़ाया, यह सुझाव दिया कि हम अपने दिमाग को खोलने पर विचार करें कि त्रिकोण क्या हो सकता है:
खैर, आपके पाठक के अनुसार, जिन्होंने 17 अतिरिक्त त्रिकोणों का उल्लेख किया (एंड्रयू का उपयोग नहीं किया) निर्दिष्ट करें कि त्रिकोण के तीन किनारों में कौन सी रेखाएं शामिल हो सकती हैं "खंड", स्पष्ट रूप से बहुत कुछ खोजने में विफल अधिक। उदाहरण के लिए, 30-जनवरी 2020 के "महत्वपूर्ण अद्यतन" परिशिष्ट में नीचे-बाएँ मिनी-त्रिकोण। क्या मिनी-त्रिभुज के क्षेत्र और उससे सटे समभुज का क्षेत्रफल एक दूसरे त्रिभुज के लिए संयुक्त नहीं होगा?
विचार के लिए एक और विचार: त्रिकोण के 3 कोण हैं (जिन्होंने अनुमान लगाया होगा?); हालाँकि, मैं यह कहूंगा कि आप एक त्रिभुज का वर्णन कैसे करते हैं, कहा जाता है कि कोण अलग-अलग त्रिकोण पैदा करेंगे। त्रिभुज T को देखते हुए, A, B, और C के साथ, t-एक को ABC द्वारा वर्णित किया जा सकता है, जिसमें B केंद्रीय कोण है। मेरा सुझाव है कि टी-दो, बीएसी द्वारा वर्णित किया जा रहा है, अलग है। इसी तरह बीसीए के लिए।
यदि हम एक विशेष मामला लेते हैं, तो समकोण त्रिभुज, हम साइन, कोसाइन और स्पर्शरेखा कार्य (SOH, CAH, TOA) प्राप्त कर सकते हैं। यदि हम उस त्रिभुज पर लागू होते हैं (और समकोण की आवश्यकता को शांत करते हैं, तो इसका मतलब यह हो सकता है कि BAC CAB से भिन्न है। बेशक, समद्विबाहु और समबाहु त्रिकोण के लिए अपवाद बनाए गए हैं (बाद वाले में केवल 3 अलग त्रिकोण परिभाषाएं होंगी)।
मैंने यह नहीं सोचा कि प्रत्येक सुझाव को कैसे निर्धारित किया जाए (और पूर्व को लागू करने के बाद गिनती बढ़ाई जाएगी अभी भी), इसलिए मेरे पास आपके लिए एक महत्वपूर्ण महत्वपूर्ण अद्यतन में उपयोग करने के लिए एक आसान संख्या नहीं है (यदि आपको मेरे विचार सार्थक लगे अपडेट करें)।
मैंने किया, जेम्स। और मुझे इंतजार रहेगा निस्संदेह, मैंने यह तय करने का फैसला किया कि कितने अतिरिक्त त्रिकोण हैं, जिससे हमारे नए अराजक नियम दिए जा सकते हैं, और 43 में पहुंचे, कुल 61:
एंड्रयू डेनियल
हालाँकि, मुझे पूरा यकीन है कि इसे पढ़ने वाला कोई भी व्यक्ति मुझे बहुत जल्दी बताएगा कि मैं अभी तक गलत हूं और फिर से सबूत दूंगा और भी अधिक छिपे हुए त्रिकोणों के कारण, मुझे लंबे और घुमावदार रास्ते पर एक और खरगोश छेद भेजना पड़ा पागलपन। (साइड नोट: मैंने तीन दिनों में अपनी पत्नी को नहीं देखा है। कृपया उसे बताएं कि मैं उससे प्यार करता हूं।) इसलिए मैं एक आखिरी चुनौती जारी कर रहा हूं: यदि आप मूल छवि में सबसे संभव त्रिकोण पा सकते हैं, तो मुझे अपना काम दिखाएं, और निश्चित रूप से साबित करें आपकी सर्वोच्चता, मैं इस कहानी को अंतिम बार अपडेट करूंगा और आपको ट्राइंगल किंग या क्वीन, अभी और ताज पहनाऊंगा सदैव। गॉडस्पीडः।

स्पीडरिपर रूबिक क्यूब
$12.45
रूबिक का घन 40 साल से लोगों को पागल कर रहा है। अपने आप को यह पता लगाने की कोशिश करें, या इसे हल करना सीखें गणित का उपयोग कर।

कनूडल 3-डी पहेली गेम
$8.79
सिर्फ 12 टुकड़ों के साथ, लेकिन 200 कुल चुनौतियों के साथ, कूडल 2-डी और 3-डी पहेली के साथ बच्चों और वयस्कों दोनों को स्टंप करेगा।

सागरदा बोर्ड गेम
$29.98
एक बेहतरीन पहेली में साल का बोर्ड गेम, आप और तीन अन्य खिलाड़ी सागरदा फमिलिया की सना हुआ ग्लास खिड़कियों को शिल्प करने का प्रयास करते हैं।

आयाम 3-डी पहेली खेल
$40.97
इस तेजी से पुस्तक 3-डी पहेली खेल में सबसे अधिक अंक अर्जित करने के लिए अपने क्षेत्रों को ढेर करने के लिए त्वरित सोच, तर्क और भाग्य का संयोजन शामिल है।
से:लोकप्रिय यांत्रिकी


